문서 간의 유사도, 즉 벡터 간의 유사도를 구하기 위해 코사인 유사도를 많이 사용한다.
코사인 유사도가 어떻게 이 수식이 나오게 되었는지 수학적으로 증명해보도록 한다.
필자는 고등학교 이후로 거의 수학을 다시 볼 일이 없었기 때문에 왜 이런 공식이 이런 형태로 되어있는지 궁금하여 정리한 글이다.
코사인 유사도
두 개의 문서를 v, u 라는 벡터로 임베딩했을 때, 두 벡터의 코사인 값은 다음과 같다.
cosθ = \frac{v⋅u}{∥v∥∥u∥}
유사도 비교하기
벡터 v 를 기준으로 v 와 u 가 비슷한지, v 와 w 가 비슷한지 cosθ 으로 판단해보자.

고등학교 때 cosθ = \frac{x}{r} 임을 배웠다.
- 두 벡터는 비슷할수록 θ 가 작아진다. (점점 가까워지므로)
- θ 가 작을수록 cosθ는 점점 커진다. (분자 값이 점점 커지므로)
- 즉, cosθ 가 클수록 더 유사하다.
따라서 v 와 u, v 와 w 의 cosθ 를 각각 계산한 후에 값이 더 큰 쪽이 더 유사하다고 판단할 수 있다.
공식 파헤치기
이런 공식은 어떻게 나왔을까?
cosθ = \frac{v⋅u}{∥v∥∥u∥}
① 벡터의 길이 구하기
※ 핵심 공식: 코사인 법칙

벡터 v, u 를 이은 대각선 길이는 ∥v-u∥ 이며, ∥v-u∥ 는 ∥v∥, ∥u∥, cosθ 로 표현할 수 있다.
(코사인 법칙은 아래 ①-②에서 자세하게 살펴본다.)
∥v-u∥^2 = ∥v∥^2 + ∥u∥^2 - 2∥v∥∥u∥ cosθ \quad (by. 코사인 법칙)
||v|| 는 벡터 v의 길이를 나타내는 기호이다.
∥v-u∥^2 = (v-u)⋅(v-u) 이므로 좌변을 아래처럼 다시 쓸 수 있다.
(왜 벡터 길이의 제곱이 자신과의 내적과 같은지는 아래 ①-①에서 자세하게 살펴본다.)
(v-u)⋅(v-u) = ∥v∥^2 + ∥u∥^2 - 2∥v∥∥u∥ cosθ
v⋅v 는 벡터 v의 내적을 나타내는 기호이다.
∥v∥^2-2vu + ∥u∥^2 = ∥v∥^2 + ∥u∥^2 - 2∥v∥∥u∥ cosθ
\therefore cosθ = \frac{v⋅u}{∥v∥∥u∥}
①-① ∥v-u∥^2=(v-u)⋅(v-u) 인 이유
※ 핵심 공식: 피타고라스의 정리, 벡터 내적
벡터 길이의 제곱은 자신과의 내적과 같다.
||v||^2 = v⋅v
벡터의 내적 계산 방식은 각 성분끼리 곱한 후 더한다.
v⋅v = (a_1, a_2)⋅(a_1, a_2) = a_1^2+a_2^2 \quad ⋅⋅⋅⋅(1번 식)
벡터 v = (a_1, a_2) 일 때, (0, 0) 에서 (a_1, a_2) 까지의 거리는 피타고라스의 정리를 이용하면 다음과 같다.

||v|| = \sqrt{(a_1-0)^2 + (a_2-0)^2} = \sqrt{a_1^2 + a_2^2} \quad ⋅⋅⋅⋅(2번 식)
1번 식과 2번 식을 합쳐보자
v⋅v = a_1^2+a_2^2 = \sqrt{a_1^2+a_2^2}^2=||v||^2
따라서 ||v||^2 = v⋅v 이고 위에서 ∥v-u∥^2=(v-u)⋅(v-u) 로 다시 쓸 수 있는 것이다.
①-② 코사인 법칙
① 벡터의 길이 구하기 에서 본 아래의 식, 어떻게 나온 걸까?
∥v-u∥^2 = ∥v∥^2 + ∥u∥^2 - 2∥v∥∥u∥ cosθ \quad (by. 코사인 법칙)

삼각형의 빗변 c는 나머지 길이 a, b 그리고 사이각 θ 로 표현할 수 있다.
점 A: (a, 0)
점 B: (bcosθ, bsinθ)
두 점 사이의 거리 c는 아래처럼 구할 수 있다.
c = \sqrt{(bcosθ-a)^2+(bsinθ-0)^2}
(왜 위의 공식이 두 점 사이의 거리인지는 ①-②-① 에서 살펴볼 것이다.)
c = \sqrt{(bcosθ-a)^2+(bsinθ-0)^2} \\ = \sqrt{b^2cos^2θ-2abcosθ+a^2+b^2sin^2θ} \\ =\sqrt{b^2(cos^2θ+sin^2θ)-2abcosθ+a^2} \\ =\sqrt{b^2-2abcosθ+a^2}
\therefore c^2=a^2+b^2-2abcosθ
벡터 v, u 사이의 거리는 ∥v-u∥ 이므로 위 식에 대입하면 이와 같이 나타낼 수 있는 것이다.
∥v-u∥^2 = ∥v∥^2 + ∥u∥^2 - 2∥v∥∥u∥ cosθ
①-②-① 두 점 사이의 거리
※ 핵심 공식: 피타고라스의 정리
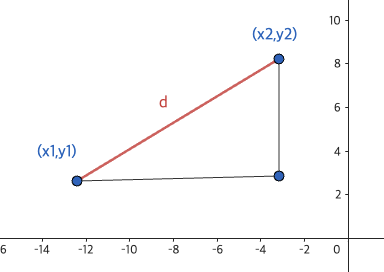
두 점 (x_1,x_2), (y_1,y_2) 를 삼각형으로 표현한 후 두 점 사이의 거리 d 를 구하려면 피타고라스의 정리를 사용한다.
d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
레퍼런스
[책] 수학 리부트
글 읽어주셔서 언제나 감사합니다. 좋은 피드백, 개선 피드백 너무나도 환영합니다.
'SearchDeveloper > 알고리즘' 카테고리의 다른 글
| [아호코라식 (Aho-corasick) 알고리즘] 논문 이해하기 (3) - 성능 측정 (2) | 2024.07.24 |
|---|---|
| [아호코라식 (Aho-corasick) 알고리즘] 논문 이해하기 (2) - 데이터 구축 (0) | 2024.04.14 |
| [아호코라식 (Aho-corasick) 알고리즘] 논문 이해하기 (1) - 검색 과정 (0) | 2024.04.12 |
| 편집 거리 알고리즘 이해하기 (0) | 2022.12.11 |
| ElasticSearch BM25 이해하기 (5) | 2022.08.25 |


